今日題目

題目連結：144. Binary Tree Preorder Traversal
題目主題：Stack, Tree, Depth-First Search, Binary Tree

前一篇提到了Heap是一個Tree的結構，這次開始正式進入Tree的世界。今天要分享如何想像 Tree 的樣子，學習如何讀這顆樹的資料。而接下來的三個題目我們是用 Depth-First Search 深度優先的方式來解題。

簡單說說 Tree

接下來會有很多題目會看到像下圖這樣的註解：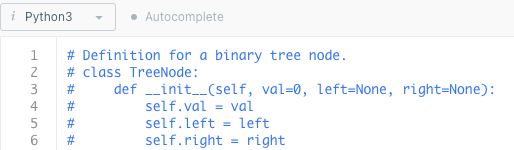

這是在說明一個樹的節點長什麼樣子，稱它TreeNode，每個節點會有三個屬性。

1. val：這個節點的值。
2. left：是一個TreeNode，這個節點的子層左節點。
3. right：是一個TreeNode，這個節點的子層右節點。

以下是一個範例，可以這樣想像：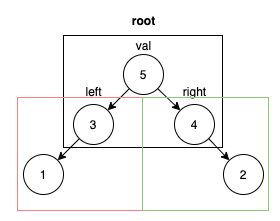

上圖中，黑色的方框是一個TreeNode，可以看到他實際的val是5，左邊紅色方框是 left 子層左節點(TreeNode)，右邊綠色方框是 right 子層右節點(TreeNode)。再以紅色方框的TreeNode為例，這是一個沒有子層右節點的TreeNode，這樣的狀況是有可能的。當然這只是一個範例，實際上一棵樹可能長的更大，最下層的 2 這個子節點下面可能還有一個left節點跟right節點這樣長下去。

另外要提的是，接下來給的題目，都會給這樣的範例，如下圖：

所以在這邊也要先分享，如何將一個陣列看成一棵樹？拿昨天的範例當例子。

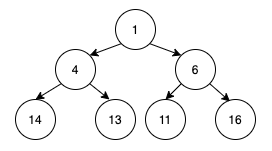
實際上這棵樹轉成陣列以後，會長這個樣子：
tree = [1, 4, 6, 14, 13, 11, 16]
那如果沒有這個圖，只有陣列時，應該要怎麼看呢？

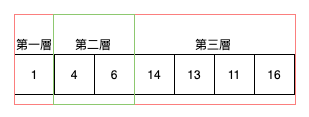
如上圖，每一層有多少數量就是用 2 的次方來看。
第一層是 2 的 0 次方，只有一個，而這個就是樹的根節點。
第二層是 2 的 1 次方是2，所以有兩個元素，分別是根節點的子層左節點及子層右節點。
第三層是 2 的 2 次方總共有四個，從左邊排到右邊，14、13 就是 4 的子節點，11、16就是6的子節點。
假設這棵樹繼續長第四層，就會是 2 的 3 次方，總共會有8個節點，依此類推。
最後再看一次對應圖。

簡單說說 Preorder Traversal

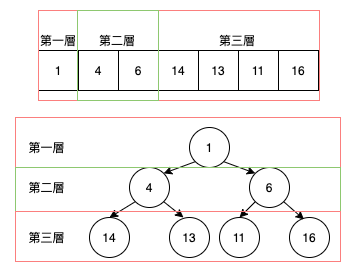
在DFS（Depth-First Search）中Traversal分成三種方式：

1. Preorder
2. Inorder
3. Postorder

今天會用到的就是Preorder Traversal。
Preorder的原則就是，進入一個節點時，馬上讀取它的值，假設資料是 tree = [5, 2, 6, 1, 3, null, 8]

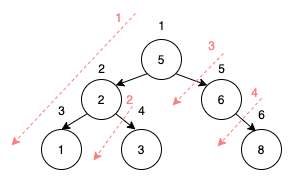
上圖中，每個節點上面的數字是讀的順序，而紅色虛線箭頭就是讀的方向。
Preorder排出來就會是 [5, 2, 1, 3, 6, 8]。

題目解說

建議可以看看LeetCode原本的題目說明，這邊是用我的方式說明題目，參考就好。

今天的題目，目標就是用Preorder的方式來讀取樹，依照Preorder的順序將節點的值排到一個列表中，最後回傳這個列表。

約束：

• 樹的節點總數範圍在 [0, 100]
• 100 <= Node.val <= 100

範例1

輸入: root = [1,null,2,3]
輸出: [1,2,3]

範例2

輸入: root = []
輸出: []

範例3

輸入: root = [1]
輸出: [1]

範例4

輸入: root = [1,2]
輸出: [1,2]

範例5

輸入: root = [1, null, 2]
輸出: [1,2]

建議到這邊先停下來，嘗試自己解解看，若沒有想法可再繼續走下去。

解題的想像

文字描述

1. 寫一個遞迴方法，這個方法要能傳入前往的節點及要完成的list。
2. 每呼叫一次這個方法會往一個節點前進，
3. 這個遞迴會一直到走到發現沒有節點才會往回走。
4. 每進入一個節點的當下會將目前節點的值紀錄到list中。
5. 最終跑完所有節點會回傳一份用Preorder排出來的list。

圖解過程

範例：tree = [5, 2, 6, null, 8]

下圖中是實際上Traversal在走的過程，實際在想像移動過程的時候，建議在最下面的節點都補虛線的節點代表走到底了。

1. step1 及 step2都直接進入了一個新節點，紅色圓就是目前要紀錄到list的數字。
2. step3 及 step4實際走到一個紅色圓，都有一個路徑，這個路徑是實際上走到紅色圓之前會先經過的節點。
3. step5 會把剩下的虛線節點走完，確認整棵樹走過一次，再走回根節點結束這個Traversal。
4. 走完step1 ~ step5以後，就會組成step6看到的list，這個list是過程中出現的紅色圓一個一個組成的，也就是Preorder Traversal最後要回傳的結果。

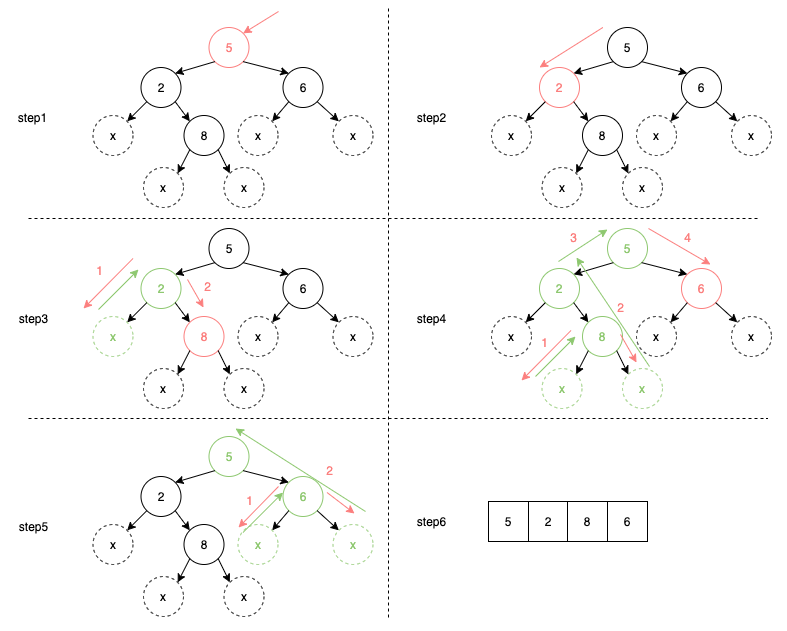
若因為沒想法而走到這邊，建議看完想像以後再給自己一次機會試一次。

程式碼撰寫

class Solution:
    # root 要進入的節點
    # preorder_list 最終要回傳的list
    def traversal(self, root: TreeNode, preorder_list: List[int]):
        # 沒有節點往回走
        if root == None: return preorder_list
        # 進入節點紀錄目前的值
        preorder_list.append(root.val)
        # 前往左邊子節點
        preorder_list = self.traversal(root.left, preorder_list)
        # 前往右邊子節點
        preorder_list = self.traversal(root.right, preorder_list)
        return preorder_list
    
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        return self.traversal(root, [])

希望您今天能瞭解到...

1. TreeNode的長相
2. 將陣列看成一個樹的結構
3. Preorder Traversal
4. 144. Binary Tree Preorder Traversal的解題方法

若內容有什麼問題或建議歡迎一起交流：）
感謝您今天願意花時間看完這篇文章~~~~

Next：94. Binary Tree Inorder Traversal